Зависимость баллистического коэффициента от формы пули

Продолжение. Начало здесь

Рождение G1

После исследований Круппа, во Франции, Гаврская комиссия с 1873 по 1898 год, провела свои собственные эксперименты, отсреляв пулю Круппа.

ЧИСЛО МАХА (по имени Эрнста Маха (1838-1916гг.), австрийского физика Безразмерная величина, равная отношению скорости газа к местной скорости звука M = V/a.

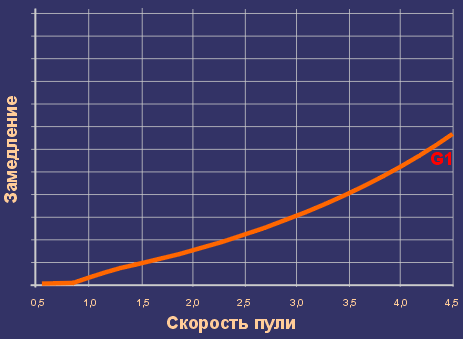
Комиссия объединила свои результаты с результатами экпериментов Круппа и составила график зависимости х ускорения (отрицательного) пули от ее скорости (в числах Маха). Другими словами, они замеряли и вычислили мгновенное отрицательное ускорение (замедление), вызванное сопротивлением воздуха, на многих точках дистанции. Получился вот такой график. У него был один недостаток - в то время еще не знали, что необходимо учитывать разницу атмосферных условий при отстреле. Называют его драг-функцией (drag-function), от английского слова drag - сопротивление. Можно перевести как функция аэродинамического или лобового сопротивления.

Дальше благодарное человечество начало пользоваться этой драг-функцией, используя ее для уничтожения себе подобных на двух последующих Мировых войнах, называя ее в честь разработчиков G-функцией (по первой букве Гаврской комиссии).

Физически, это была таблица, которая состояла из двух колонок. Первая - это скорость в футах в секунду (или числах  Маха). Вторая - значение функции Gv. Для страдающих бессоницей, методика вычисления, на английском здесь

Постоянный баллистический коэффициент

Как видно на графике, график аэродинамического сопротивления пули другого, чем у пули Круппа (стандартной пули) веса и диаметра имеет абсолютно ту же форму, только повернут относительно графика стандартной пули.
То есть замедление тестируемой пули изменяется прямопропорционально замедлению стандартной пули.
Если пуля легче или меньше по диаметру, чем стандарная пуля, то график ляжет выше, так как такая пуля замедляться (терять скорость) будет быстрее, а значит отрицательные мгновенные ускорения будут больше по значению.

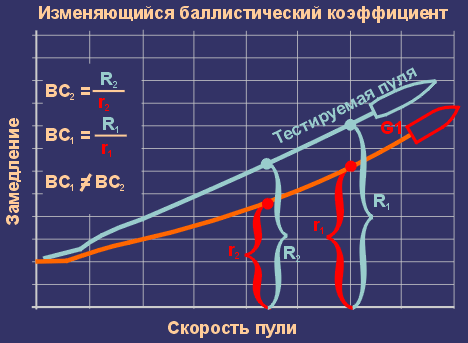
Было введено понятие баллистический коэффициент, которое по смыслу отражало угол, на который этот график был повернут относительно графика стандартной пули.
Значение баллистического коэффициента вычислялось как :

где
BC - Баллистический коэффициент,
r - замедление стандартной пули
R - замедление тестируемой пули

или, по графику, разница координат

BC = R₁ / r₁

Теперь, зная баллистический коэффициент определенной пули, можно было вычислить ее собственную драг-функцию, а затем и ее траекторию.

Вычисление баллистического коэффициента

Баллистический коэффициент находится по формуле:

где
W - вес пули в фунтах,
d - диаметр пули в дюймах,
i - форм-фактор (коэффициент формы пули или драг-коэффициент или коэффициент аэродинамического сопротивления)

Если ввести понятие поперечная плотность (sectional density), равную SD = w / d², то формула примет такой вид:

BC = SD/i

По этой формуле работает калькулятор баллистического коэффициента №1. В нем только пять самых распространенных форм-факторов. Формула не учитывает форму хвостовой части пули.

Также существует формула вычисления баллистического коэффициента на основе формулы Arthur Pejsa, предложенной им в 1983 году. Она учитывает форму хвостовой части пули.
Калькулятор №2 баллистического коэффициента по форме пули, написанный на основе формулы Arthur Pejsa.

Вычисление замедления пули

Найдя баллистический коэффициент, замедление (retardation) стандартной пули вычисляется по одной из формул, разнообразие которых соответствует количеству баллистических теорий.

Вот, например, формула, разработанная в Британии с 1904 по 1906 годы:

R = Av^m = BC * r = pg
^{откуда замедление тестируемой пули:}
r = Av^m / BC
 

где

Кстати, выражение Avm зачастую обозначают как Gv ,то есть: Gv = Avm, а общая формула примет вид: r = Gv / BC, где Gv и есть "та самая" G-функция

R  - замедление стандартной  пули, футы/сек²
r  - замедление тестируемой пули, футы/сек²

v  - скорость тестируемой пули, футы/сек

m - степень

A = константа

BC - баллистический коэффициент

p - сила сопротивления воздуха

g - гравитационная константа

Появление проблемы

Позже, после второй Мировой войны, в Баллистической исследовательской лаборатории армии США (US Army's Ballistics Research Lab) слегка модернизировали G-функцию (в первой колонке - значение скоростей в в числах МАХа, во второй - коэффициент аэродинамического сопротивления), учли влияние атмосферных условий и начали исследовать появившуюся проблему.

Суть ее была в следующем. G-функция исправно работала на протяжении более полувека до тех пор, пока не появились пули другой формы, отличающейся от стандартной пули Круппа. Когда они замеряли пулю с конической хвостовой частью (boat-tail), то оказалось, что график аэродинамического сопротивления совершенно другой (смотри рисунок).

То есть форма кривой не идентична графику стандартной пули, а значит, замедление тестируемой пули на различных скоростях было не прямо пропорционально замедлению стандартной пули

В сложившейся ситуации есть два решения:
1. Вычислять и применять для каждой пули множественные баллистические коэффициенты
2. Разработать новую G-функцию для этого типа пуль.

Решение 1. Больше моделей

Они пошли сначала по второму пути и разработали новую G-функцию со стандартной пулей с конической хвостовой частью (наклон конуса 7° 30' ) и тангенсной оживальной частью радиусом 6,19 калибра.
Для того, чтобы их различать, Гаврскую G-функцию с этого момента начали называть G1, а новую - G5.

А другие формы пуль, спросите вы? А для других тоже нужны свои G-функции. Часть из них была создана в той же лаборатории:

Математические модели полета пуль
	G1 - Стандартная модель, основанная на пуле Круппа
G2	нет данных
	G5 - для пули с конической хвостовой частью (наклон конуса 7° 30' ) и тангенсной оживальной частью радиусом 6,19 калибра
	G6 - Для пуль с плоской хвостовой частью и тангенциальной оживальной частью радиусом 6,99 калибра (Spire Point).
	G7 - Для пуль с длинной конусной хвостовой частью (угол 7° 30') и секантной оживальной частью радиусом 10 калибров
G8	G8 - Для пуль с плоской хвостовой частью и секантной оживальной частью радиусом 10 калибров
	GS - Модель для круглой пули
RA4	Для калибра .22LR (идентична G1 на скоростях ниже 426 метров в секунду)
GL	Модель для полуоболочечных пуль(идентична G1 на скоростях ниже 426 метров в секунду)
GI	переработанная таблица Ингалса

НО! Баллистический коэффициент какой-то определенной пули будет постоянен на всех скоростях только если ее форма будет ТОЧНО соответствовать стандартной пуле какой-нибудь из уже разработанных драг-функций. На практике это трудно достижимо. Разнообразие форм пуль настолько велико в настоящее время, что сделать для них для всех свои драг-функции вряд ли представляется возможным.

Решение 2. Множественный баллистический коэффициент

В 1981 году на базе результатов, полученных ученым Баллистической исследовательской лаборатории армии США (US Army's Ballistics Research Lab) Робертом МакКоем (Robert L. McCoy) была создана математическая модель, позволяющая вычислять драг-функцию для пули любой формы. Его отчет, датированный 1981 годом, можно почитать на английском (файл формата PDF, 3,2 Мб). В отчете также присутствет исходный текст программы на Фортране, созданной Билом Дэвисом (Bill Davis), из компании Tioga Engineering.
А это позволяло вычислять траекторию, не используя ни одну из существующих G-функций и, следовательно, не пользуясь понятием баллистический коэффициент.

Но, на практике, когда производитель продает изготовленные пули, ему надо как-то указывать характеристики пули. Как правило, указывается баллистический коэффициент по модели G1. Но, если форма пули не совпадает с формой пули Круппа, то BC будет переменным.

Программа позволяет вычислить баллистический коэффициент (по модели G1 и G7) пули любой формы для любой скорости. Такой программой для конструирования пуль пользуется известный Daniel Lilja и также в сети есть версия этой программы, написанная на языке Perl (доступна по адресу: Bullet Drag and Twist). Я сначала пользовался этим калькулятором, но результаты, которые он выдавал, вызывали сомнения из-за использования  драг-функций, отличных от первоисточника. Пришлось написать свой калькулятор, основанный на исходном тексте, опубликованном у Daniel Lilja.

Пример. Пули патронов 7Н1 и ЛПС

Как же будет изменяться баллистический коэффициент относительно скорости для пули, форма которой не соответствует, например таблице G1?

С помощью Калькулятора №3 баллистического коэффициента по форме пули, вычисляем зависимость BC (G1) пуль патронов 7Н1 и ЛПС от скорости. Получается вот такой график.

Видно, как пуля ЛПС проигрывает 7Н1 на дозвуковых скоростях, за счет менее конусной хвостовой части, но это же, видимо, дает ей преимущество на скоростях от 400 до 700 м/сек. Также видно, как на трансзвукоых скоростях за счет турбулентных потоков происходит рост аэродинамического сопротивления (коэффициента) и, соответственно, падение баллистического коэффициента.

Кстати:
Какой BC для своей пули сообщает нам производитель? BC для начальной скорости? Какой-то усредненный? Если это компания Sierra, дающая усредненный BC для трех или четырех диапазонов скоростей, то как, по какому принципу они его усредняют?

Разница результатов

1. Вычислим траекторию пули 7Н1 в трех разных баллистических моделях. Причем BC в моделях G1 и G7 вычислим с помощью того же калькулятора, а BC по модели G6 получим конвертацией, которую может делать баллистический калькулятор Ballistic Explorer.

Абсолютное снижение пули патрона 7Н1 расчитанное в различных моделях, см
 

По форме пуля ближе всего к стандартной пуле модели G6, поэтому резонно предположить, что траектория, рассчитанная с помощью модели G6, наиболее близка к истине. Приняв это, можно видеть, что отклонение результатов в модели G1 на ближних дистанциях незначительно, но на дистанции 1000 метров уже составляет около 8,5 %.

2. Теперь посмотрим разницу траекторий при применении постоянного BC, рассчитанного для начальной скорости и множественного BC. Множественный BC получен расчетом средних значений BC на указанных в таблице диапазонах скоростей, причем максимальная скорость (Max) взята 1200 м/сек.
 

Абсолютное снижение пули патрона 7Н1 расчитанное с постоянным и множественным коэффициентом, см
 

Применение постоянного баллистического коэффициента, вычисленного только для начальной скорости дает траекторию:
на 700 метров - ниже на 16 см (2,8%)
на 1000 метров - ниже на 67 см (4,5%)
по сравнению с вычислениями, основанными на множественном BC.

С другой стороны, траектория с постоянным коэффициентом ближе по значениям к траектории G6, чем траектория с множественным BC. Наверное, способ усреднения BC должен быть какой-то другой.

К сожалению, большинство баллистических калькуляторов работают только с одним баллистическим коэффициентом. И только некоторые, например Ballistic Explorer, позволяют вводить несколько BC для различных диапазонов скоростей, а также переводить BC одной модели в другую.

Выводы

1. Баллистический коэффициент любой отдельно взятой пули не является постоянной величиной почти всегда.

2. Разница в применяемых моделях становится значимой на больших дистанциях.

3. По сравнению с вычисленным по форме пули, теоретическим баллистическим коэффициентом, реальный баллистический коэффициент будет от него отличаться. Как правило, в меньшую сторону, Из-за рыскания пули, которая не учитывается в расчетах, но увеличивает аэродинамическое сопротивление, из-за качества изготовления самой пули (ее поверхности в том числе), конкретной температуры, высоты над уровнем моря при стрельбе и шага нарезов ствола винтовки.

4. Самым верным способом определения траектории пули, несмотря на все теоретические изыскания, остается практический отстрел конкретного боеприпаса из конкретной винтовки

Калькулятор баллистического коэффициента пули, фактора гироскопической стабильности и оптимального шага нарезов