Шаг нарезов

Начало

Нарезы, как известно, служат для того, чтобы, получив от них вращательное движение (угловую скорость), пуля приобрела гироскопическую устойчивость в полете. Устойчивость выражается через расчет фактора гироскопической стабильности (ФГС) или статической стабильности.

Гироскопическая стабильность пули

(Источник - yellowba.gif (226 bytes) How do bullets fly?)

Фактор гироскопической стабильности должен быть больше единицы и выражается формулой:

,

где

Коэффициент опрокидывающего момента

d

диаметр пули

Ix

Осевой момент инерции пули

Iy

Поперечный момент инерции пули

Плотность воздуха (зависит от температуры, давления и влажности)

vw

линейная скорость пули (с учетом ветра)

угловая скорость пули

Калькулятор фактора гироскопической стабильности пули

Конструкторы винтовок и пуль предпочитают, чтобы этот фактор был около 1,2...1,5. Когда значение ФГС превыщает 1,5 - это называют перестабилизацией пули. Дело в том, что с увеличением угловой скорости:
растет деривация (рыскание) пули;
падает траекторная устойчивость - пуля начинает вести себя как гироскоп, нос ее поднимается. Особенно это сильно проявляется при выстреле под большим углом к земной поверхности.

ПРИМЕР:

Пуля M80 выпущена из ствола с шагом нарезов 1:12 под углом 32 градуса. При вылете из ствола коэффициент статической стабильности равен 1,35. Видно, как после 3000 метров наступает резкое снижение статической стабильности.

 

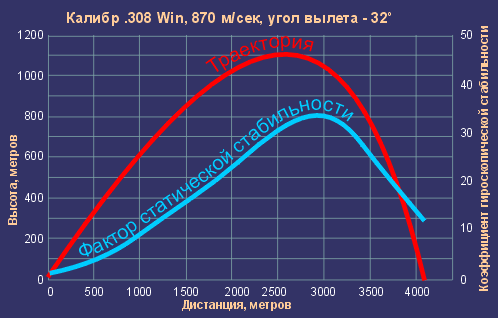
Вывод 1. Так как линейная скорость пули находится в знаменателе, а угловая скорость - в числителе и угловая скорость пули снижается значительно медленнее, чем линейная, то по мере удаления пули от ствола гироскопическая стабильность пули растет, но, с некоторого момента, резко падает. Поэтому кучность при увеличении дистанции может меняться нелинейно. То есть, определенная пуля может показывать хорошую кучность на коротких дистанциях и плохую на длинных. И наоборот.

Вывод 2. Чем больше угловая скорость пули, тем больше статическая стабильность пули, но хуже динамическая (см. выше).

Вывод 3. Понижение плотности воздуха, вследствие повышения температуры или повышения высоты над уронем моря, повышает стабильность пули. И наоборот.

Формула Гринхила

Для определения соответствия размеров пули шагу нарезов существует эмпирическая формула Гринхила. Она была выведена в 1879 году сэром Гринхилом (Alfred George Greenhill, жил 1847-1927). Впервые она была опубликована в Британском учебнике стрелкового оружия (British Textbook of Small Arms)  в 1929 году. Позволяет для заданного калибра и заданной  пули рассчитать оптимальный шаг нарезов.

T = шаг нарезов в дюймах
K = константа Гринхила = 150 (для нач.скорости пули от 457 до 853 м/сек) и 180 - для нач.скорости пули свыше 853 м/сек и 125 - для пистолетов. Данные значения константы справедливы для свинцовых пуль с оболочкой из меди или ее сплава. Константа жестко привязана к плотности материала пули и если бы мы задумали стрелять из алюминиевых пуль - константа была бы другая.
D = диаметр пули в дюймах
L = длина пули в дюймах

шаг нарезов при заданной длине пули:

T = (K * D2) / L

или при уже заданном шаге нарезов длина пули:

L = (K * D2) / T

Например:

Для пули калибра .308, длиной 1,35 дюйма (вес 200 гран или 13 грамм) получаем:

(150 * 0,3082) / 1,35 = 10,54

Получаем приблизительно шаг нарезов 1:10,5 (10,54 дюймов на совершение полного оборота пули в стволе), что близко к используемому в винтовках калибра 30-06 шагу нарезов 1:10.

Если диаметр пули и ее длину брать в метрической системе, т.е в миллиметрах, константа НЕ МЕНЯЕТСЯ. Таким образом:

(150 * 7,822) / 34,29 = 267,51 мм

Калькулятор шага нарезов по формуле Гринхила

Исходные данные:

Константа (обычно 150) :

Диаметр пули, дюймов :

Длина пули, дюймов :

Результаты:

Шаг нарезов, дюймов :

Выводы

Вывод 1: Главную роль в стабилизации пули в играет ее длина, а не вес.

Вывод 2: Более длинные пули для стабилизации требуют более быстрых нарезов (меньшего шага нарезов)

Вывод 3: Шаг нарезов в изготавливаемоей винтовке выбирается по самой длинной (тяжелой) пуле, которая будет применяться в данном калибре.

Вывод 4: Можно стрелять из ствола более легкими пулями, чем теми, на которые он рассчитан, без ущерба траекторной устойчивости и кучности. Если стрелять более тяжелыми, чем расчетные - пуля будет недостабилизирована. Говоря проще, пуля будет "кувыркаться"...

Формула компании Sierra Bullets

T = 0,06 * V * D2 / L,

где

V - начальная скорость пули, фут/сек
T = шаг нарезов в дюймах
D = диаметр пули в дюймах
L = длина пули в дюймах

Например:

Для пули калибра .308, длиной 1,35 дюйма, начальная скорость 800 м/сек получаем:

0,06 * 2624 * 0,3082 / 1,35 = 11, 063

 

 Угловая скорость пули

Угловую скорость пули грубо можно оценить по формуле:

w = V/(T * 0,0254), 

где
w - угловая скорость пули, об/сек;
V - начальная скорость пули, м/сек;
T - шаг нарезов в дюймах

Например:

Начальная скорость 935 м/сек, шаг нарезов - 1:12.

Получаем:

935/(12 * 0,0254) = 3 067,5 об/сек

 

Существует эмпирическое правило для грубого определения стабильности пули  - по ее угловой скорости. Пуля должна вращаться с угловой скоростью не менее 170 000 об/мин или 2833 об/сек. Цифра эта приблизительна и, на самом деле, у конкретной пули угловая скорость для оптимальной ее (пули) стабилизации может быть и 140 000 об/мин и 200 000 об/мин, в зависимости от ее веса и формы.

Для вычисления угловой скорости можно воспользоваться калькулятором.

Типовой шаг нарезов в популярных калибрах

Рекомендуемые шаги нарезов в зависимости от калибра и веса пули

Ссылки

WinGyro программа для расчета фактора гироскопической стабильности

Calibers & Twists рекомендуемый шаг нарезов для разных калибров и весов пуль

 

Оружие > Баллистика нарезного оружия

Автор не несет никакой ответственности за любой вид ущерба, понесенного в результате использования присутствующей здесь информации. Автор оставляет на усмотрение читателя, применять полученные здесь сведения, или подвергнуть тщательной проверке в специализированных источниках.

www.ada.ru